Çocuklar Nasıl Matematik Öğrenir – Matematik öğrenmek, bilim ve teknolojiye adapte olmak için son derece önemlidir. Günümüzde teknoloji ve bilişim alanlarının ne kadar önemli olduğu düşünülürse, matematik bilmek ve öğrenebilmek ayrı bir öneme sahiptir. Her ne kadar bu önemin farkında olmayanlarımızın sayısı az olsa da ülkemizde matematik başarısı ne yazık ki istenilen seviyede değildir. Ancak matematik öğrenme güçlüğü sadece ülkemize özgü bir durum değildir. Bu nedenle matematik öğrenme güçlükleri pedagojik anlamda birçok defa incelenmiştir.
Araştırma sonuçlarının ortak vurgu noktası çocukluk yıllarının matematik başarısında son derece önemli olduğudur.
Çocukluk yılları özellikle sayıların öğrenildiği ve sayılar arasındaki ilişkilerin keşfedildiği yıllardır. Bu matematiksel temel, sonraki yıllarda matematik başarısı için belirleyici olmaktadır. Çocuklar sayıları öğrenirken beyinlerinde nasıl bir etkileşim olduğunu bilmek, matematik başarılarını arttırmak için son yıllarında üzerinde çalışılan önemli konuların başında gelmektedir.
Bu makaleyle matematik öğrenmenin düşünsel anlamda oluşturduğu potansiyelin sinir sistemimiz üzerinde ne anlama geldiğini öğreneceksiniz. Ayrıca matematiğin sadece yaşamımız için değil sinir sistemi için de ne kadar özel olduğunu fark edeceksiniz. Bu farkındalığın oluşması için yapılan önemli araştırmalara birlikte bir göz atalım:
Çocuklar Matematiği Hangi Beyin Alanlarını Kullanarak Öğrenirler?
Çocuklar Nasıl Matematik Öğrenir – Stanford Üniversitesi’nden Tanya M. Evans, John Kochalka ve ekibinin 2015 yılında yaptığı çalışmada çocukların sayısal yeterlilik ve beyin yapıları arasındaki ilişkileri ortaya koyan çalışmaları önemli yenilikleri de ortaya çıkarmıştır;
Yaptıkları çalışmada Evans ve ekibi, başlangıçta yapısal ve fonksiyonel MRI kullanılarak beyinleri taranan 43 çocuktan oluşan grubun bireysel farklılıkları öngören yapısal ve içsel bağlantı ölçülerini araştırmak için 9 ve 14 yaşları arasındaki çocukları çoklu zaman noktalarında görüşmeler ve testler yaparak değerlendirmişlerdir. İlk çocukluk yıllarından ergenliğe kadar olan dönemde sayısal öğrenmenin beyin yapıları arasındaki ilişkileri sistematik olarak incelemişlerdir.
8 yaşında çocukların beyinlerinde “Ventrotemporal Oksipital Kortex (VTOC)”, “Posterior Parietal Kortex (PPC)” ve “Prefrontal Kortex’i (PFC)” içerecek şekilde gri maddenin hacminin uzunlamasına büyümesinin belirgin şekilde artarak sayısal düşünme becerilerinin geliştiği gözlemlenmiştir (Bahsi geçen beyin bölgelerinin yerleri ve görevleri aşağıda verilmiştir).
“Posterior Parietal”, “Anterior Temporal” ve “Dorsolateral Prefrontal” Kortekslerle VTOC bağlantısı, sayısal yeteneklerdeki bireysel kazanımları sağlayan en geniş ağ olarak ortaya çıkmıştır (Dehaene and Cohen, 1995; Ansari, 2008; Menon, 2014). Ayrıca bu bölgeler ek olarak “cuneus” ve “premotor” korteksi de içerdiği görülmüştür (Yazının devamında motor kortex ve aritetik arasındaki bağlantı daha detaylı olarak açıklanacaktır).
Yapılan çalışma, ilk kez insan beyninde sayısal becerilerin gelişimini destekleyen fonksiyonel devreleri tanımlamakta ve öğrenme güçlüğü riski altındaki çocukları tanımlamak için potansiyel bio belirteçleri vurgulamaktadır.
Çalışmanın diğer bir özelliği ise beyindeki matematik öğrenme yapılanmasının kendine özgü olduğu ve beyinde oluşan en uzun bağlantı yapısına sahip olduğu görülüştür. Hatta çalışmanın detaylarında okuma veya çalışan hafızadaki (working memory) bireysel kazanımları içermeyecek şekilde sonuçların ortaya çıktığı görülmüştür. Bu da tanımlanan ağın özgüllüğünü vurgulamıştır. Yani beynin matematik becerisi için özel bir gelişim sistematiğine sahip olduğu görülmüştür.
Ventro Temporal Oksipital Cortex (VTOC) : İnsan beynindeki ventral nesne görme yolu, neredeyse sınırsız çeşitlilikteki bireysel yüzler ve nesneler için farklı temsiller üretme kapasitesine sahiptir. Yüzleri, nesneleri tanımamız için son derece önemli görevleri vardır.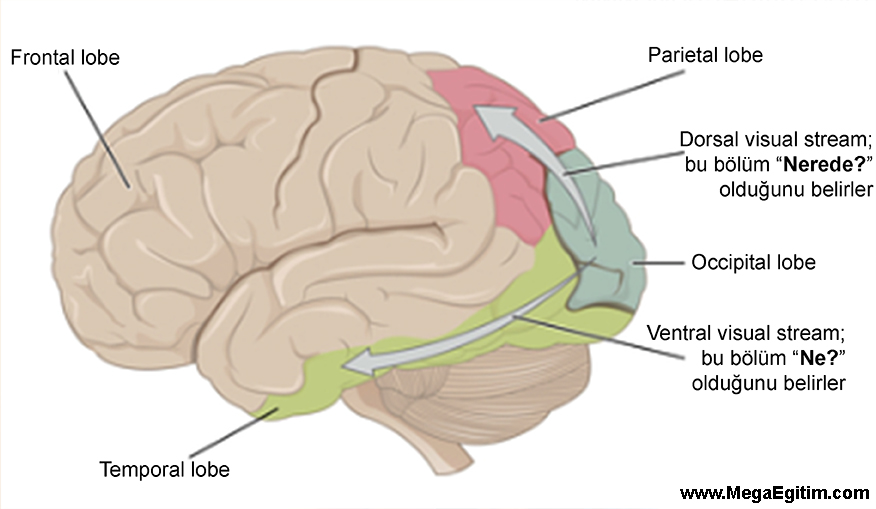
Şekil 1. Açık yeşil renkle boyanmış bölge Ventro Temporal bölgeyi göstermektedir.
Posterior Parietal Corteks (PPC) : Ventral ve dorsal görsel yollara yayılan bu posterior beyin bölgeleri, sayısal miktar gösterimi ve yönetilmesi algısal ve anlamsal yönlerinde kritik roller oynamaktadır (Dehaene et al., 2003; Piazza et al., 2007; Ansari, 2008; Cohen Kadosh et al., 2008; Glezeret al., 2009).
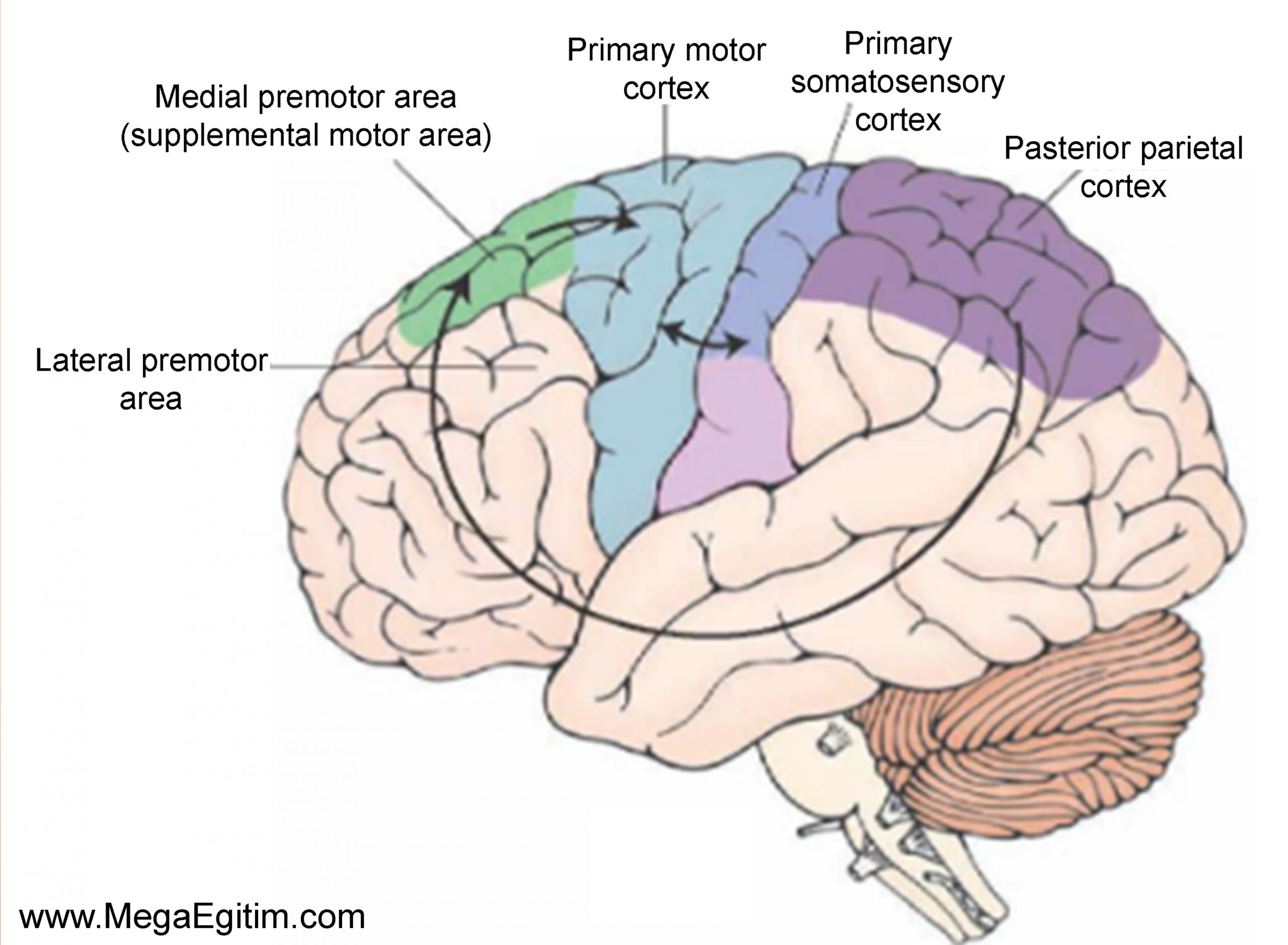
Şekil 2. Mor renkle boyanmış bölge Posterior (Arka) Parietal Cortex’i göstermektedir.
Prefrontal Korteks (PFC) : Anterior insula, ventrolateral PFC (VLPFC) ve dorsolateral PFC (DLPFC) dahil olmak üzere çoklu prefrontal korteks (PFC) bölgeleri, zahmetli sayısal hesaplama prosedürlerini yönetir Kaufmann et al., 2011).
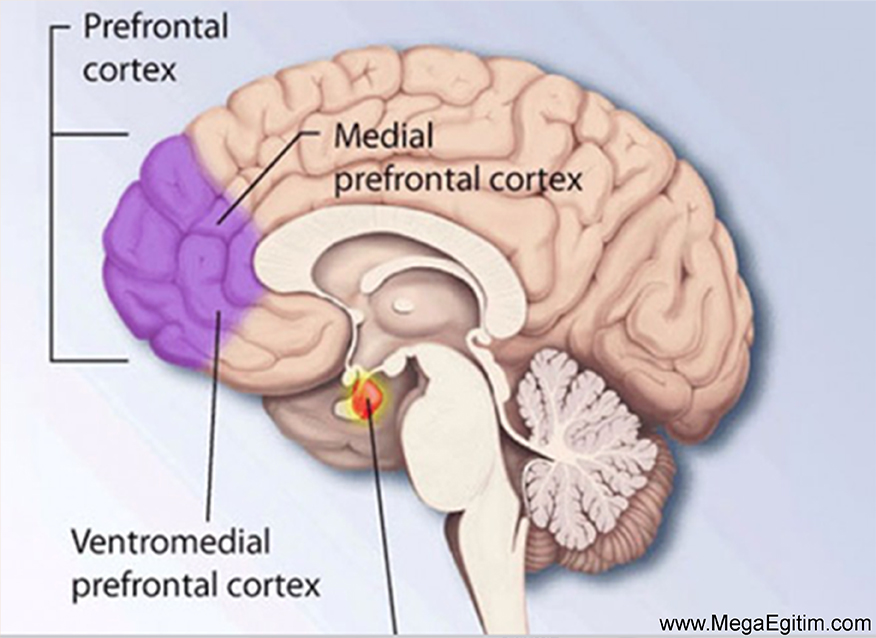
Şekil 3. Eflatun renkle boyanmış bölge Prefrontal Cortex’i göstermiştir.
Sayısal bilişin nöro gelişimsel çalışmaları, beyin aktivasyonunda çocukluktan yetişkinliğe doğru anterior-posterior (ön – arka) kaymayı ortaya çıkarmıştır, PFC’ye (ön alın lobu, aritmetiksel işlemleri yapmakla sorumlu olan beyin alanı) artan güven, deneyim ve yeterlilik ile VTOC ve PPC’nin artan katılımı ile karakterize edilmiştir. Burada çocukluktan ergenliğe geçiş döneminde matematikle ilgilenen beyin bölgelerinin genişlediğini göstermiştir. Eklenen beyin bölgeleri görsel ve üç boyutla ilgili verileri de işleyen beyin bölgeleridir. Buradaki geçiş eğitim psikolojisinde somut işlem döneminden soyut işlem dönemine geçiş olarak da kategorize edilmektedir.
Peki yapılan bu eşsiz çalışmadan nasıl sonuçlar çıkmaktadır?
Çocuklar Nasıl Matematik Öğrenir – İnsan beyni matematik öğrenirken en ön lobundan en arkada yer alan görsel oksipital lob bağlantılarına kadar uzunlamasına bir gelişim göstermektedir. Beyindeki bu en uzun bağlantılı yapı, karar verme ve analiz yeteneğine sahip olan ön alın lobunu, motor hareketleri (beden hareketlerini) kontrol eden premotor korteksi, boyut ve derinlik algımızı yöneten parietal korteksi, görsel lobun bir parçası olan ventro temporal oksipital korteksi içermektedir.
Bu yapı matematik öğrenmenin tek düze olamayacağını göstermektedir. Hatta beyindeki matematiksel alan, okuma ve çalışan hafızadan bağımsız bir yapısal gelişim ortaya koymaktadır. Bu sonuçlar ülkemizde olduğu gibi diğer birçok ülkede de matematik öğrenme güçlüğünün nedenlerini ortaya koymaktadır;
Ülkemizde sınav odaklı bir öğrenme olduğundan öğrenciler matematik öğrenme yöntemi olarak sadece benzer çözüm yöntemlerine dayalı çokça problem çözmeyi benimsemişlerdir. Bu uygulama yoğun işlem ve analiz yapan ön alın lobu ve dil becerileri ile ilgili olan temporal bölgeyi içermektedir. Ancak dikkat ederseniz beynin matematik öğrenebilmek için oluşturduğu uzunlamasına gelişim yapısı bu çalışma yöntemiyle desteklenemeyecektir. Matematik becerisinin gelişebilmesi için uzay, boyutlar ve görsellik gerekmektedir. Bu başlı başına yeni bir matematiksel öğrenme sistemine geçilmesi demektir.
Çocukluktan itibaren dokunma ve boyut ile ilgili tasarlanan matematiksel öğrenme araçlarıyla çalışmalar yapılmalıdır. Gelişimin, uygun dönemde sağlanması yaşanabilecek öğrenme güçlüklerini önlemek adına son derece önemlidir. Aksi durumlarda yaşanan öğrenme güçlüklerinin matematik öğrenmeye karşı olumsuz tutum geliştirilmesine neden olduğu bilinmektedir. Bu ise matematik öğrenmeyi olabildiğince zorlaştırmaktadır.
Araştırmaların ortaya koyduğu bu kritik dönemde yapılaması gereken önemli faaliyetler olduğu açıkça görülmektedir;
- Sayılar, görsel ve boyut içeren egzersizlerle çocuklara öğretilmelidir.
- Üç boyutlu düşünmeyi, uzay-mekansal zekayı geliştirebilecek zeka oyunları veya oyuncakları ile tasarlanmış faaliyetlere çocukların katılmaları sağlanmalıdır.
- Sürekli kağıt üstünde problem çözmeye dayalı bir matematik öğrenme sistemi yerine problemleri görsel ve simülasyonlar ile ifade eden sistemlerle çocukların karşılaşması sağlanmalıdır.
- Matematiksel kavram, formül ve ifadeler olabildiğince görsellerle gösterilmelidir.
Beyinde Aritmetik ve Parmakların Bağlantısı Nedir?
Çocuklar Nasıl Matematik Öğrenir – Sayısal bilişin nöro gelişimsel çalışmalarından öğrendiğimiz önemli bulgulardan bir diğeri ise sayısal yeteneğin gelişimde premotor cortex’in önemli bir role sahip olduğudur. Özellikle son yıllarda yapılan çalışmalarda parmak gelişimiyle aritmetik yeteneğinin gelişiminin bağlantılı olduğunu gösteren birçok bulgu yer almaktadır.
Özellikle yaşanan beyin lezyonları sonucunda birlikte kaybedilen aritmetik yeteneği ve parmak fonksiyonları nöro gelişimsel ortaklığı göstermektedir. Gerstmann Sendromu, bu ortaklığı gösteren en önemli kanıtların bir tanesidir;
Dr. Gerstmann tarafından ilk kez 1924 yılında 52 yaşındaki bir kadın hastada görülen klinik durum Gerstmann Sendromu olarak tanımlanmıştır. Bu hastanın hafıza ve yazma güçlüğü şikâyetleri tespit edilmiştir. Ayrıca nörolojik muayenesinde ise sağ hemianopsi (Görme alanının bir yarısını kapsayan körlük hali), hesap yapma güçlüğü, vücudunun sağ-sol tarafını tanıma bozuklukları belirlenmiştir. Sonraki yıllarda görülen bazı vakalarda apraksi (beyinden gelen mesajın konuşma kaslarına doğru şekilde iletilememesi sonucunda ortaya çıkan motor konuşma bozukluğu) ve renk algılama sorunu bulunmuştur.
1930 yılında Gerstmann, incelediği tüm vakaları değerlendirerek “Gerstmann Sendromu” olarak adlandırdığı yeni sendromu; akalkuli (beyin hasarı veya yaralanması sonucu basit matematik hesaplamalarını yapamama), agrafi (yazma yeteneğini kaybetme), sağ-sol ayırım bozukluğu, parmak agnozisi semptom kompleksi olarak tanımlanmıştır. Parmak agnozisi, el parmaklarını fark etme, tanıma, isimlendirme, ayırma, seçme ve hissetme yeteneğinin kaybı sendromu olarak tanımlanmıştır. Sendrom sol angular gyrus lezyonlarına bağlı geliştiği bildirilmiştir Köseoğlu, Akgül, Kendirci, 2014).
Not: “Akalkuli” ile “Diskalkuli” ifadeleri bazen karışıklık yaşanmasına sebep olmaktadır. “Akalkuli” ile “Diskalkuli” arasındaki fark şudur: “Diskalkuli” beyinde bir hasar olmadan matematik öğrenme veya matematik işlemlerde problam yaşamak iken; “Akalkuli” beyin hasarlı bir hastanın daha önceden matematik becerilerinde problem yok iken, beyin hasarı veya yaralanması sonucu matematiksel becerilerde zorlanmasıdır.
Şekil 4. Turuncu renkle boyanmış bölge Angular Gyrus’u göstermiştir.
Gerstmann Sendromu, sayısal yetenekle parmaklar arasındaki bağlantıyı gösteren bulguları ilk defa ortaya koymuştur.
Çocuklarda Parmakla Saymak Bir Gereklilik midir? Ya da Gelişimsel Bir Engel midir?
Çocuklar Nasıl Matematik Öğrenir – Gerstmann sendromu tarihte ilk kez insan nörolojik sisteminde bilişsel bir öğrenme alanı ile bedensel faaliyetler arasında bağlantı olabileceğini ortaya koymuştur. Özellikle sayma eyleminin parmakla yapıldığı çocukluk dönemi özellikle incelenmeye değer bulunmuştur. İlk çocukluk ve ergenlik başlangıcı öncesi süreçte parmakları kullanarak aritmetik yapmak ve saymak, soyut işlem dönemine geçilmemiş olan dönemde kavramları somutlaştırmak için önemli bir eylem olduğu yönünde birçok bilimsel çalışma yapılmıştır.
Yapılan çalışmaların orjinini parmak agnosisi (parmak hassasiyeti) ve sayma yeteneği ilişkisi oluşturmaktadır. Ayrıca, parmak temsillerinin sembolik olmayan miktarlar ve sembolik sayılar arasında bağlantılar sağladığı düşünüldüğünden, parmak agnosisinin kendi başına görsel – mekansal yetenek ve hesaplamada parmak kullanımı ile ilişkili olup olmadığını belirlemek önemlidir.
Robert Reeve ve Judihumberstone 2011 yılında 5 ve 7 yaşlarında olan çocuklar üzerinde yaptıkları çalışmalarında sayma ve hesaplama yeteneğinin geliştirilmesinde parmakların ilişkisini araştırmışlar ve okul öncesi dönemde parmakla saymanın gelişimsel olarak bir gereklilik mi yoksa bir engel mi olduğu sorusuna yanıt aramışlardır.
5 ila 7 yaş arasında değişen 30 çocuk üzerinde yapılan çalışmada, çocukların parmak hassasiyeti, görsel-uzamsal çalışma belleği ve matematik performansı test edilmiştir. Çalışma sonuçlarında parmak hassasiyeti ile sayarken parmak kullanımı ve problem çözme başarısı arasında güçlü bir ilişki olduğunu göstermektedir. Ayrıca parmak kullanımı görsel-uzamsal çalışma belleğinin gelişimine öncülük ettiği görülmüştür.
Parmak Agnosisi ve Matematik İlişkisi
Bulgular ilk kez parmak agnosisi temsillerinin 5-7 yaş arasında değiştiğini göstermiştir ve değişiklik hesaplamada parmak kullanımı ile ilişkilendirilmiştir. Parmak ayırt etme yeteneğinin okul öncesi döneme göre parmakla işlem yapılan birinci sınıfta arttığı da gözlemlenmiştir. Çalışma sırasında uygulanan testlerde düşük puan alan çocukların düşük parmakla hesap yetenekleri olduğu gözlemlenmiştir. Bu sonuç, zayıf parmak agnosisinin zayıf aritmetik performans ile ilişkili olduğunu gösteren önceki çalışmaları desteklemektedir.
Çalışmanın önemli bulgularında bir tanesi de mekânsal yetenek ve sayı yeterliliği arasında önemli ilişkiler olduğunu göstermesidir. Küçük çocuklarda görsel-mekansal çalışma belleğinin tek basamaklı sayıları toplama yetenekleri ile sistematik olarak ilişkili olduğunu göstermiştir. Bu bulgu çocuklarda, hesaplama kabiliyetinin görsel-mekansal çalışma belleği ve parmak hassasiyeti gelişimleri üzerinde bağımsız olarak etkili olduğunu düşündürmektedir.
Robert Reeve ve Judihumberstone’un yaptıkları bu önemli çalışmanın sonuçları şu şekilde özetlenebilir;
- Parmak hassasiyeti, parmakları tanımlama ve ayırt etme yeteneğinin gelişiminin çocuklarda aritmetik işlemleri parmakla yaparak geliştiği gözlenmiştir.
- Çocuklarda hesaplama yaparken parmak kullanmak sayısal yeteneği, görsel-mekansal çalışan belleği geliştirmektedir.
- Bu nedenle çocuklarda sayarken ve hesaplama yaparken parak kullanmak bilişsel gelişimleri için bir gerekliliktir. Çocukların parmakla saymalarını engellemek onların zihinsel gelişimlerine olumsuz etki yapmak demektir.
Üniversite Öğrencileri Üzerinde Yapılan Deney
Stanford üniversitesinden Joe Booler’ın, üniversite öğrencileri üzerinde yaptıkları çalışmalarda yüksek parmak hassasiyetine sahip olan öğrencilerin matematik başarılarının da daha yüksek olduğunu söylemiştir. Ancak eğitimcilerin bu konuda yeterli bilgiye sahip olmadıklarını ve parmakla hesaplamayı yasaklayarak öğrencilerin sayısal gelişimlerine engel olduklarını belirtmiştir (Aşağıda verilen kısa video filmi izleyiniz).
Çocuklar Nasıl Matematik Öğrenir – Dünya Hafıza Olimpiyatları Kurucu Üyesi Melik Duyar da parmak gelişimi ve zihinsel gelişim arasındaki bağlantının farkında olduğunu ve kurduğu “Paritmetik (Parmakla Aritmetik)” sistemi ile 5-12 yaş arasındaki çocukların bilişsel gelişimlerine katkıda bulunduklarını ifade etmiştir. Sistemli olarak yapılan egzersizlerle çocukların hem sayısal-bilişsel özellikleri gelişirken hem de dikkat ve odaklanma yeteneklerinde ciddi gelişmeler olduğunu gözlemlediklerini belirtmiştir.
Melik Duyar’ın, “Paritmetik™ (Parmakla Aritmetik)”, “Fotografik Hafıza Teknikleri”, “Mega Soroban™” ve “Mega Zeka Oyunları”nı harmanlayarak oluşturduğu “ANZAN™ Mega Aritmetik Beyin Egzersizleri ve Zeka Oyunları” eğitim programı öyle başarılı olmuştur ki, sistem Çin, Singapur, Kazkistan, Özbekistan, Birleşik Arap Emirlikleri, Hollanda, Kolombiya ve Meksika gibi yaklaşık 18 ülkede Mega Hafıza lisansı altında uygulanmaktadır. Mega Hafıza bu çalışmasıyla sadece Türkiye’deki değil, dünyadaki diğer çocukların matematiksel gelişmelerine de katkıda bulunmaktadır.
Sonuç olarak yapılan araştırmalar matematik gelişiminin beyinde diğer birçok gelişim sürecinden bağımsız olarak gerçekleştiği ve ön alın lobundan arka görsel labun uzantılarına kadar uzanan boylamsal bir gelişim gösterdiğini ortaya koymuştur. Ayrıca çocuklarda sayısal bilişsel özellikler görsel-uzamsal belekle parmak hassasiyeti ve parmakla aritmetiksel işlem yapmanın son derece önemli bağlantılar içerdiği görülmüştür. Bu da çocukların zihinsel gelişimleri için parmakla sayma ve hesaplama yapmalarının desteklenmesi gerektiğini ortaya koymuştur.
Gelecekte sayısal ve üç boyutlu düşünme yeteneği yüksek bireyler yetiştirmek için çocukların bilişsel gelişim süreçlerini destekleyen eğitimler almalarını sağlamak biz yetişkinlerin en büyük görevidir. Bu görevin sorumluluğu ile çocuklarınızla sağlıklı ve başarılı yıllar geçirmenizi temenni ediyorum.
Bilgiyle kalın.
Soner Polat – Araştırmacı / Yazar
Kaynaklar
- Tanya M. Evans, John Kochalka, Tricia J.Ngoon, Sarah S. Wu, Shaozheng Qin, Christian Battista, Vinod Menon (2015) Brain Structural Integrity and Intrinsic Functional Connectivity Forecast 6 Year Longitudinal Growth in Children’s Numerical Abilities.
- Dehaene S, Cohen L (1995) Towards an anatomical and functional model of number processing. Math Cogn 1:83–120.
- Ansari D (2008) Effects of development and enculturation on number rep- resentation in the brain. Nat Rev Neurosci 9:278 –291.
- Menon V (2014) Arithmetic in child and adult brain. In: Handbook of mathematical cognition. Oxford: Oxford UP.
- Dehaene S, Piazza M, Pinel P, Cohen L (2003) Three parietal circuits for number processing. Cogn Neuropsychol 20:487–506. Medline,
- Piazza M, Pinel P, Le Bihan D, Dehaene S (2007) A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron 53:293–305. CrossRef Medline.
- Cohen Kadosh R, Lammertyn J, Izard V (2008) Are numbers special? An overview of chronometric, neuroimaging, developmental and comparative studies of magnitude representation. Prog Neurobiol 84:132–147. Medline.
- Glezer LS, Jiang X, Riesenhuber M (2009) Evidence for highly selective neu- ronal tuning to whole words in the “visual word form area.” Neuron 62:199 –204. CrossRef Medline.
- Kaufmann L, Wood G, Rubinsten O, Henik A (2011) Meta-analyses of de- velopmental fMRI studies investigating typical and atypical trajectories of number processing and calculation. Dev Neuropsychol 36:763–787. CrossRef Medline.
- Köseoğlu, N. Akgül, M. Kendirci (2014), Gerstmann Sendromlu Bir Hastada Saptanan Mental Rotasyon Bozukluğu ve Önemi.
- Robert Reeve, Judi Humberstone (2011), Five- to 7-year-olds’ finger gnosia and calculation abilities.